Most of our rounding methods are based on arithmetic rounding.
Please refer to the nomenclature described in Residue Class Rounding. So we can base our rounding on a metric and the most obvious choice is the absolute value of the difference of the two parameters, . That is what everybody does and nothing else really comes to our mind when we are talking about rounding. But this approach is based on the additive structure of our field or ring containing the numbers that we want to round. Another way of looking at this is that (in case we are talking of real numbers or some subset thereof) the choice of the rounded value is mostly based on seeing on which side of a boundary between the two candidates for the rounded values the original value lies, with special handling if it is exactly equal to this boundary. Now the this boundary is the arithmetic mean between the two candidates, therefore we call this arithmetic rounding. Just to give you an example:
We look at the „middle“ between two allowed numbers, for example usually something like when rounding a number between
and
to integers and automatically assume that above that middle we round up, below we round down and exactly on the boundary we need additional rules. This middle is the arithmetic mean of the two neighboring allowed numbers after rounding and hence we can call this arithmetic rounding. All numbers
with
are rounded to two, all numbers
with
are rounded to three.
Means
We assume and
, so each real number should be rounded to an integral number. Also we assume
.
Now assume we have a non-integral number and an integral number
such
. For convenience we write
. Then we round
to
if
and to
if
, so
serves as boundary. Now there are many other ways to define a mean between two number
and
. Some of the most common are
- arithmetic mean:
- geometric mean:
- harmonic mean:
- quadratic mean:
- cubic mean:
- generalized mean:
- arithmetic-geometric mean: Let
Then we have the AGM
- harmonic-geometric mean (also called geometric-harmonic mean): Can be defined in a similar way, by just replacing the geometric mean by the harmonic mean.
- contraharmonic mean is not so hard to understand, find it in Wikipedia.
- logarithmic mean is not so hard to understand, find it also in Wikipedia.
We could also define a arithmetic-harmonic mean in a similar way, but that is just the geometric mean. It is an interesting way to approach the geometric mean of matrices, which is somewhat hard to define otherwise because of the non-commutative multiplication.
For the users of spreadsheets, like included in LibreOffice, OpenOffice or MS-Office, you can find the arithmetic mean as function average, the geometric mean as geomean and the harmonic mean as harmean.
Others means can be defined along these lines. And we can see that:
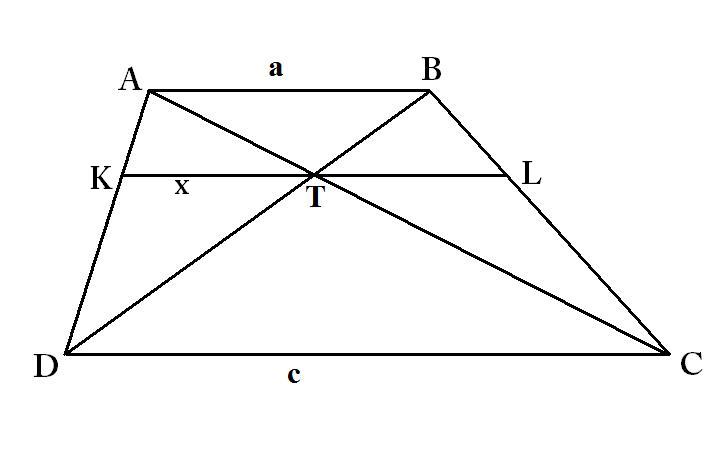
Here is a visual explanation of arithmetic, geometric and harmonic mean:
The line from K to L has the harmonic mean of
and
as a length. The geometric mean would be reached by moving that line to a position that the upper and lower part have the same shape, apart from scaling. And the arithmetic mean would be reached by moving K and L to the middle points of the lines AD and BC, respectively.
The ruby-gem long-decimal supports all of these methods for calculating a mean.
Using means to define rounding methods
Just to give you an idea that you can extend this further, the geometric and harmonic mean are now considered.
As can be seen negative and zero values for and
are causing some trouble or require some care. Actually we can deal with this by splitting our unrounded and rounded worlds into separate parts, here we take the number
, the
and the numbers
as three different sets and do the rounding within them:
with
where we define
and
and
In a similar way we define ,
and
and define metrics
,
,
separately. Then we just look at one partition
and consider rounding to be a mapping
such that is minimal.
The obvious assumption of rounding to
releaves us from dealing with logarithms of zero or division by zero. We would see that anyway any number between
and
would be rounded to
for both harmonic and geometric rounding, because the boundary is 0, if we pick the right variant of the formula for calculating the mean. Also between
and
everything is rounded to
in our example. Otherwise the calculation of the boundary can be made to work, because then both factors are negative, so we draw the square root of a positive product, but then we need to replace the square root by its negative counterpart.
So for geometric rounding we define that is rounded to
if
, rounded to
if
and rounding for
has to be defined by additional rules. But we define
for negative values of
and
to be
. This can also be expressed in terms of a metric:
and
Harmonic rounding is definable in a similar way:
We define that is rounded to
if
, rounded to
if
and rounding for
has to be defined by additional rules. This can also be expressed in terms of a metric:
and
Quadratic and Cubic rounding can be defined in a similar way. It would even be possible to go for arithmetic-geometric rounding or harmonic-geometric rounding, but that would imply having to do an approximative iterative calculation of the boundary each time it is needed, while the rounding modes described above can still be achieved with relatively simple multiplication and addition operations.
In any case it is necessary to define the rule how to round numbers that lie exactly on the boundary, unless we can prove that the boundary is irrational.
That is the case for geometric, quadratic and cubic rounding, because if we have adjacent integers and
then we see that
is irrational for
because
and
cannot both be squares, so there is one prime number that divides either
or
with an odd multiplicity, which already ensures that the square root is irrational. For the quadratic mean we have
, where the numerator of the fraction is odd, so two occurs with an odd multiplicity, which makes it irrational again. The similar argument applies for the cubic mean. For the harmonic mean we have
, where
can be a power of
, in which case we have to deal with the boundary issue.
The ruby-gem long-decimal supports geometric, harmonic, quadratic and cubic rounding in addition to the regular arithmetic rounding, that is referred to as „half“.
Harmonic and geometric rounding are important for some of the mechanisms of rounding with sum.
Based on this basis these algorithms will look more natural and no longer like some weird approach that needs to be copied from some untrusted source just to get over the nightmare of having to solve that issue.

Schreibe einen Kommentar